Chris and Trudy

While chatting with patrons at Zeno's recently, Maggie introduced two newcomers to the group gathered.

"I'd like you meet Chris and Trudy, who are visiting the Coffeehouse and who have learned about our interest in challenging puzzles and logic. They are renowned logicians, who, allegedly, are able to correctly deduce any derivable truth from any set of assumptions. So Charles and I have arranged the following, to set up our current Zeno's Challenge: We have selected two integers (not necessarily unique) such that each is within some specified range (we have kept these integers a secret between us). We now give Chris the sum of these two integers [which they do], and give Trudy the product of these two integers [which they provide]."

After receiving these numbers, Chris and Trudy do not have any communication at all except the following dialogue in the Coffeehouse:

  1. Trudy: "I do not know the two numbers."
  2. Chris: "I knew that you didn't know the two numbers."
  3. Trudy: "Now I know the two numbers."
  4. Chris: "Now I know the two numbers."

Maggie adds, "Given that the above statements are absolutely truthful, can anyone deduce the two numbers that Charles and I selected for Chris and Trudy?"

 

As faithful logical patrons, can you shed some light on this challenge?   ....Ron Barnette, Zeno's Proprietor

Please submit your reasoned answer here:

 

Name:
E-Mail:
URL:
City: , State: Country:

Comments:

*

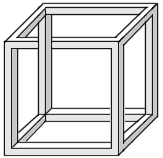
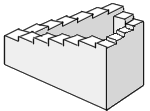
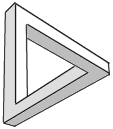
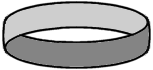
For your continued enjoyment, I thought I'd keep these so-called Impossible Objects on here, as you contemplate the new challenge. I continually receive positive comments from many loyal Coffeehouse patrons. If you locate other good ones, please let me know. Enjoy!...Ron Barnette

 

Some Impossible Objects

I credit Jim Loy for these marvelous example of so-called impossible objects, which should amuse you faithful Zeno's patrons, who appreciate thought-provoking stimulation.

Freemish crate 1. Asymmetric crate. An M. C. Escher creation, I surmise
Penrose staircase 2. The Penrose staircase: Often drawn by M. C. Escher. Clockwise is downstairs forever.
tribar 3. The tribar: Another impossible object by R. Penrose. It's hard to know how to color it, as the interior becomes the exterior.
Penrose triangle 4. The Penrose triangle: Another famous impossible object by R. Penrose. This is sometimes called a tribar (see #3, above).
ambihelical hexnut 5. An ambiguous ring...What is the outside? The inside?