Maggie's Road Trip

Maggie has a challenge that she wants Zeno's patrons to help resolve. Charles thinks that he has the solution, but she is skeptical. Please help!!!

 Maggie set out in her auto which travels downhill at a great speed, 90 mph (miles per hour), and then uphill at 72 mph, and then 80 mph on flat ground. Her auto road trip takes 3 hours to travel from Dunedin to Tallahassee. The return trip takes 3 and a half hours. Challenge: Find the distance, in miles, between the two towns ?

------------------------------------------------------------------------------------------------------------------------------------------------

For your ongoing enjoyment, I have retained these so-called Impossible Objects on here, as you contemplate the new challenge. I continually receive positive comments from many loyal Coffeehouse patrons. If you locate other good ones, please let me know. Please do this for our many visitors. Enjoy!...Ron Barnette

Some Impossible Objects

I credit Jim Loy for these marvelous example of so-called impossible objects, which should amuse you faithful Zeno's patrons, who appreciate thought-provoking stimulation. And further thanks go to Aaron Sloman, for this wonderful link to the Swedish artist Oscar Reutersvaard, who predates Penrose and Escher! 
 http://www.sandlotscience.com/EyeonIllusions/Reutersvard.htm

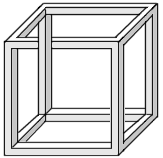
		1. Asymmetric crate. An M. C. Escher creation, I surmise
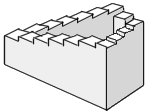
		2. The Penrose staircase: Often drawn by M. C. Escher. Clockwise is downstairs forever.
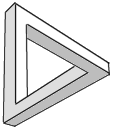
		3. The tribar: Another impossible object by R. Penrose. It's hard to know how to color it, as the interior becomes the exterior.
		4. The Penrose triangle: Another famous impossible object by R. Penrose. This is sometimes called a tribar (see #3, above).
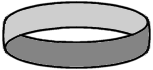
		5. An ambiguous ring...What is the outside? The inside?